สวัสดีครับแฟนเพจที่รักทุกๆ ท่าน
หัวข้อในวันนี้จะเกี่ยวข้องกันกับหัวข้อ การคำนวณทางด้านกลศาสตร์โครงสร้าง (STRUCTURAL MECHANICS COMPUTATION หรือ SMC) นะครับ
วันนี้ผมจะขออนุญาตมาเอาใจน้องๆ ที่เป็นนักศึกษาทางด้านสาขาวิศวกรรม เช่น วิศวกรรมโยธา วิศวกรรมเครื่องกล วิศวกรรมอุตสาหกรรม เป็นต้น โดยที่ผมจะมาแนะนำวิธีในการคำนวณหาค่าแรงดัดในโครงสร้างคานแบบที่สามารถคำนวณได้โดยวิธีอย่างง่าย (DETERMINATE BEAM) ไม่ว่าจะเป็นค่าบน แผนภาพแรงเฉือน (SHEAR FORCE DIAGRAM) และ แผนภาพโมเมนต์ดัด (BENDING MOMENT DIAGRAM) ด้วยเทคนิคง่ายๆ ที่หากน้องๆ และ เพื่อนๆ จำไปใช้ ก็น่าที่จะเป็นประโยชน์ในการวิเคราะห์โครงสร้างของทุกๆ คนได้นะครับ
เทคนิคนี้ก็คือ การคำนวณหาค่าบน แผนภาพแรงดัด จากการคำนวณพื้นที่ของ แผนภาพแรงเฉือน นะครับ ซึ่งจริงๆ แล้วเทคนิคนี้ก็มีที่มาที่ไปมาจากหลักการพื้นฐานทางด้านกลศาสตร์โครงสร้างในเรื่องของหลักการในการคำนวณหาค่าแรงเฉือนและแรงดัดในโครงสร้างนะครับ ซึ่งในโอกาสต่อๆ ไปผมจะขออนุญาตนำมาขยายความให้แก่เพื่อนๆ ทุกๆ คนอีกครั้งก็แล้วกันนะครับ
โดยหลักการง่ายๆ ของวิธีการนี้ก็คือ หากเราทำการคำนวณหาแผนภาพแรงเฉือนได้แล้ว เราสามารถที่จะทำการคำนวณหาค่าบนแผนภาพแรงดัดได้จากการคำนวณพื้นที่ของแผนภาพแรงเฉือนได้เลยโดยตรงตามหลักการทางเรขาคณิตทั่วๆ ไปได้เลยนะครับ และ เพื่อเป็นการไม่เสียเวลา เรามาดู ตย ที่ผมเตรียมมาเลยดีกว่านะครับ
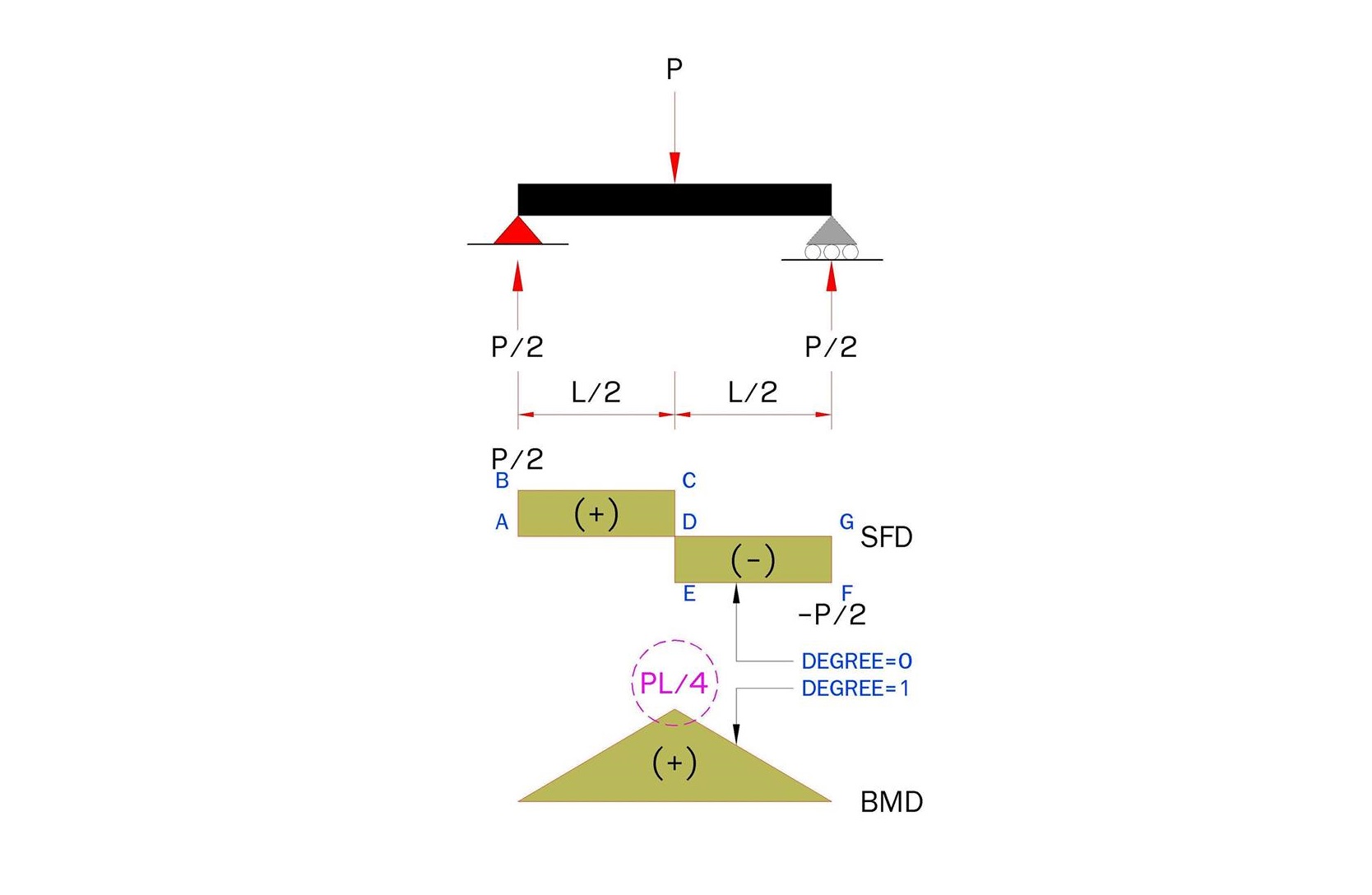
ตย ข้อนี้เป็นคานช่วงเดียว (SIMPLE SPAN BEAM) รับ นน แบบกระทำเป็นจุด (CONCENTRATED LOAD) ที่กึ่งกลางช่วงของคาน
หากพวกเราจำได้คานช่วงเดียวที่รับ นน แบบนี้จะมีค่าโมเมนต์ดัดสูงสุดที่กึ่งกลางช่วงเท่ากับ
M max = PL/4
เราจะมาดูวิธีในการคำนวณหาค่าแรงดัดด้วยเทคนิคนี้ไปพร้อมๆ กันเลยนะครับ
เริ่มต้นจากเราต้องทำการคำนวณหาค่าแรงปฏิกิริยาของคานเสียก่อนนะครับ ซึ่งสำหรับคานแบบนี้แรงปฏิกิริยานั้นก็จะง่ายๆ ตรงไปตรงมานะครับ คือ เท่ากับ
R left = R right = P/2
ขั้นตอนต่อมา คือ เราต้องทำการคำนวณและเขียนแผนภาพแรงเฉือนออกมาให้ได้นะครับ ซึ่งใน ตย ข้อนี้เราสามารถที่จะทำได้ง่ายๆ เลยนะครับ เริ่มจากจุด A ก่อนก็แล้วกันนะครับ ที่ตำแหน่งนี้จะมีแรงกระทำในทิศทางขึ้นเท่ากับแรงปฏิกิริยาที่ตำแหน่งนี้เท่ากับ P/2 ไปจนถึงตำแหน่ง B จากนั้นจากจุด B ไปจุด C นั้นไม่มีแรงใดๆ กระทำบนคานเลย จึงทำให้แผนภาพแรงเฉือนนั้นเป็นเส้นตรงเพราะว่าค่าแรงเฉือนบนคานนั้นคงที่ไม่เปลี่ยนแปลงนะครับ จากนั้นที่จุด C จะมีแรงกระทำในทิศทางลงเท่ากับ P ทำให้ในที่สุดที่ค่าแรงเฉือนที่ตำแหน่ง E จะมีค่าเท่ากับ P/2 – P = -P/2 และจากนั้นช่วง E ถึง F ก็จะเหมือนกันกับช่วง B ถึง C นะครับ คือ ไม่มีแรงใดๆ กระทำบนคานเลย จึงทำให้แผนภาพแรงเฉือนนั้นเป็นเส้นตรงเพราะว่าค่าแรงเฉือนบนคานนั้นคงที่ไม่เปลี่ยนแปลง และ ตำแหน่งสุดท้ายที่ตำแหน่ง F จะมีแรงกระทำในทิศทางขึ้นเท่ากับ P/2 ทำให้ในที่สุดค่าแรงเฉือนที่ตำแหน่ง G นั้นมีค่าเท่ากับ 0 เพราะ –P/2 + P/2 = 0 นั่นเองนะครับ
มาถึงขั้นตอนสุดท้าย คือ ทำการคำนวณหาค่าแรงดัดจากแผนภาพของแรงเฉือน ซึ่งในรูปแผนภาพแรงเฉือนใน ตย ข้อนี้ของเราจะพบว่ามีสี่เหลี่ยมสองรูปที่มีขนาดเท่าๆ กัน คือ สี่เหลี่ยมด้านบน ABCD และ สี่เหลี่ยมด้านล่าง DEFG เพราะ คานของเรามีลักษณะสมมาตร ทำให้เวลาทำการคำนวณค่าแรงดัดแล้วในที่สุดค่าแรงดัดสุดท้ายจะต้องมีค่าเท่ากับ 0 นะครับ
เรามาคำนวณพื้นที่ของสี่เหลี่ยม ABCD กันนะครับ โดยที่สี่เหลี่ยมรูปนี้จะมีค่าเป็น บวก เพราะรูปๆ นี้อยู่ทางด้านบนนะครับ โดยที่สูตรในการคำนวณพื้นที่สี่เหลี่ยม คือ กว้าง คูณ สูง โดยที่ ความกว้าง ของสี่เหลี่ยมจะมีค่าเท่ากับ L/2 และ มี ความสูง ของสี่เหลี่ยมจะมีค่าเท่ากับ P/2 ดังนั้นเราก็จะสามารถทำการคำนวณหาค่าแรงดัดที่กึ่งกลางช่วงของคานได้เท่ากับ
∑M = M1 = (กว้าง)(สูง) = (L/2)(P/2) = PL/4
จากนั้นรูปสี่เหลี่ยมที่สอง คือ สี่เหลี่ยม DEFG ซึ่งจะมีค่าเป็น ลบ เพราะรูปๆ นี้อยู่ทางด้านล่างก็จะมีค่าเท่ากันกับสี่เหลี่ยม ABCD แต่มีเครื่องหมายตรงกันข้ามกัน ทำให้ผลรวมของค่าแรงดัดจะมีค่าเท่ากับ
∑M = M1 + M2 = PL/4 + [– (L/2)(P/2)] = PL/4 – PL/4 = 0
เล่ามาถึงตรงนี้ผมเชื่อว่าคงที่จะมีเพื่อนๆ หลายๆ คนสงสัยว่าแล้วเราจะทราบได้อย่างไรว่ารูปทรงของ แผนภาพแรงดัด นั้นจะเป็นรูปทรงใด ?
ในตอนท้ายนี้ผมจึงเทคนิคเล็กๆ อีกเทคนิคหนึ่งจะมาแนะนำในการเขียนแผนภาพแรงดัด คือ ค่าความชันของแผนภาพแรงดัดนั้นจะมีค่า เพิ่มขึ้น จากแผนภาพแรงเฉือนเท่ากับ 1 ดีกรีเสมอ เช่น ใน ตย ข้อนี้จะเห็นได้ว่าแผนภาพแรงเฉือนนั้นเป็นเส้นตรง ซึ่งจะมีค่าความชันเท่ากับ 0 ดังนั้นแผนภาพแรงดัดก็จะมีค่าความชันเท่ากับ 0 + 1 = 1 ซึ่งก็คือ เป็นเส้นตรง นั่นเองนะครับ
เป็นไงบ้างครับ เทคนิคนี้ค่อนข้างที่จะทำได้ตรงไปตรงมา สามารถที่จะคำนวณได้ง่ายๆ เลยใช่มั้ยครับ ก็หวังว่าน้องๆ และ เพื่อนๆ ทุกคนจะสามารถจำจดจำเทคนิคนี้ไปใช้ในการวิเคราะห์โครงสร้างคานกันได้นะครับ
หวังว่าความรู้เล็กๆน้อยๆ ที่ผมได้นำมาฝากแก่เพื่อนๆ ทุกๆ ท่านในวันนี้จะมีประโยชน์ต่อทุกๆ ท่านไม่มากก็น้อย และ จนกว่าจะพบกันใหม่นะครับ
ADMIN JAMES DEAN
บริษัท ภูมิสยาม ซัพพลาย จำกัด ผู้นำกลุ่มธุรกิจเสาเข็มสปันไมโครไพล์ รายแรกและรายเดียวในประเทศไทย ที่ได้การรับรองมาตรฐาน ISO 45001:2018 การจัดการอาชีวอนามัยและความปลอดภัย การให้บริการตอกเสาเข็ม The Provision of Pile Driving Service และได้รับการรับรอง ISO 9001:2015 ของระบบ UKAS และ NAC รายแรกและรายเดียวในประเทศไทย ที่ได้รับการรับรองระบบบริหารงานคุณภาพ ตามมาตรฐานในกระบวนการ การออกแบบเสาเข็มสปันไมโครไพล์ การผลิตเสาเข็มสปันไมโครไพล์ และบริการตอกเสาเข็มเสาเข็มสปันไมโครไพล์ (Design and Manufacturing of Spun Micropile/Micropile and Pile Driving Service) Certified by SGS (Thailand) Ltd.
บริษัท ภูมิสยาม ซัพพลาย จำกัด คือผู้ผลิตรายแรกและรายเดียวในไทย ที่ได้รับการรับรองคุณภาพ Endoresed Brand จาก SCG ด้านการผลิตเสาเข็ม สปันไมโครไพล์ และได้รับเครื่องหมาย มาตรฐาน อุตสาหกรรม มอก. 397-2524 เสาเข็มสปันไมโครไพล์ Spun Micro Pile พร้อมรับประกันผลงาน และความเสียหายที่เกิดจากการติดตั้ง 7+ Year Warranty เสาเข็มมีรูกลมกลวงตรงกลาง การระบายดินทำได้ดี เมื่อตอกแล้วแรงสั่นสะเทือนน้อยมาก จึงไม่กระทบโครงสร้างเดิม หรือพื้นที่ข้างเคียง ไม่ต้องขนดินทิ้ง ตอกถึงชั้นดินดานได้ ด้วยเสาเข็มคุณภาพมาตรฐาน มอก. การผลิตที่ใช้เทคโนโลยีที่ทันสมัย จากประเทศเยอรมัน เสาเข็มสามารถทำงานในที่แคบได้ หน้างานสะอาด ไม่มีดินโคลน เสาเข็มสามารถรับน้ำหนักปลอดภัยได้ 15-50 ตัน/ต้น ขึ้นอยู่กับขนาดเสาเข็มและสภาพชั้นดิน แต่ละพื้นที่ ทดสอบโดย Dynamic Load Test ด้วยคุณภาพและการบริการที่ได้มาตรฐาน เสาเข็มเราจึงเป็นที่นิยมในงานต่อเติม
รายการเสาเข็มภูมิสยาม
1. สี่เหลี่ยม S18x18 cm.
รับน้ำหนัก 15-20 ตัน/ต้น
2. กลม Dia 21 cm.
รับน้ำหนัก 20-25 ตัน/ต้น
3. กลม Dia 25 cm.
รับน้ำหนัก 25-35 ตัน/ต้น
4. กลม Dia 30 cm.
รับน้ำหนัก 30-50 ตัน/ต้น
(การรับน้ำหนักขึ้นอยู่กับสภาพชั้นดินในแต่ละพื้นที่)
☎ สายด่วนภูมิสยาม:
082-790-1447
082-790-1448
082-790-1449
081-634-6586
? Web:
bhumisiam.com
micro-pile.com
spun-micropile.com
microspunpile.com
bhumisiammicropile.com