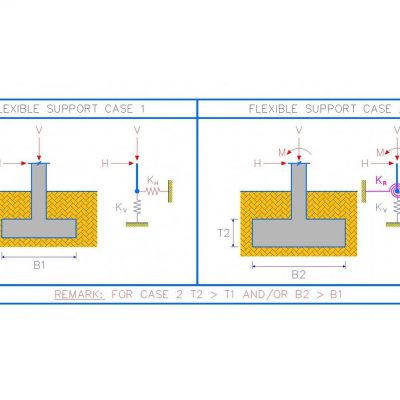
FLEXURAL FORMULA ในเรื่อง STRESSES IN BEAM
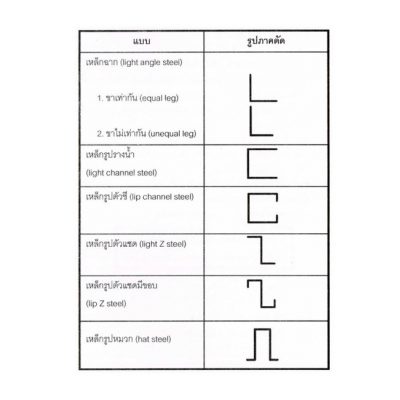
สาเหตุที่ผมหยิบยกเรื่องๆ นี้มาฝากแก่เพื่อนๆ เพราะว่าผมเห็นว่าในหลายๆ ครั้งเพื่อนๆ มักไม่ได้นำความรู้ รวมไปถึงค่าต่างๆ ในหัวข้อนี้ไปใช้ในการวิเคราะห์ความเค้นในคานกันสักเท่าใดเลยนะครับ เพราะ เพื่อนหลายๆ คนมักจะมีความเข้าใจว่าในการหาค่าความเค้นในคานเราจำเป็นที่จะต้องทำการวิเคราะห์หาแรงปฏิกิริยาของจุดรองรับ หาค่าโมเมนต์ดัด และ จากนั้นเราจึงจะสามารถทราบได้ว่าคานนั้นจะมีความเค้นดัดเกิดขึ้นในหน้าตัดเป็นค่าเท่าใด เอาเป็นว่าวันนี้ผมจะมาให้คำแนะนำกับเพื่อนๆ ก็แล้วกันนะครับว่าการหาความเค้นดัดในคานนั้นเราไม่จำเป็นที่จะต้องทำเช่นนั้นก็ได้นะครับ เรามาเริ่มต้นดูรูปที่ผมแนบมาด้วยประกอบคำอธิบายของผมกันเลยดีกว่านะครับ
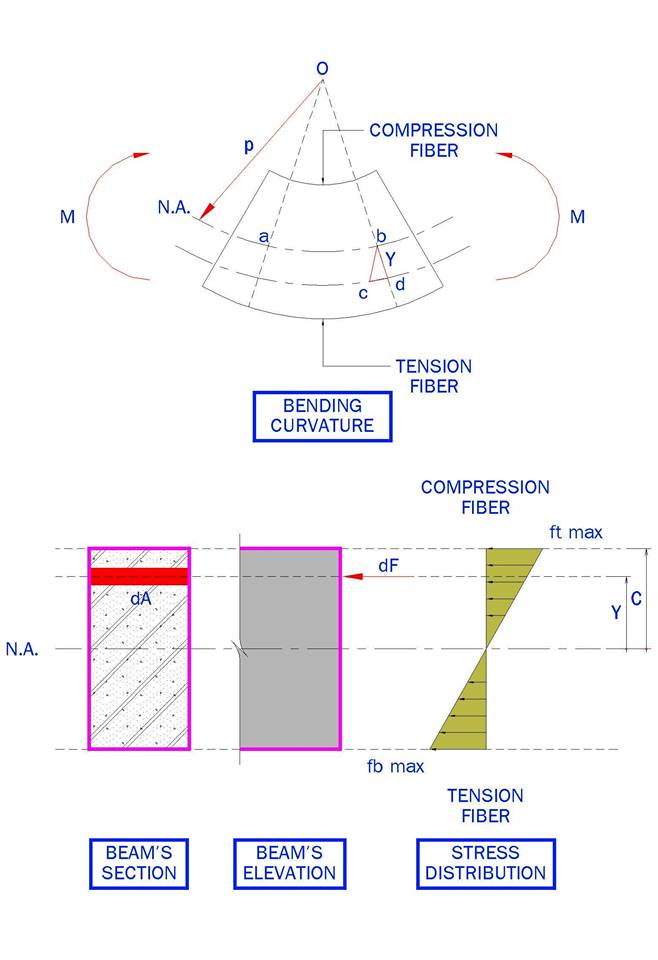
ก่อนอื่นผมขออธิบายก่อนนะครับว่าทฤษฎีที่ผมจะกล่าวถึงต่อไปนี้เป็นทฤษฎีที่ว่าด้วยการที่คานนั้นมีค่าการโก่งตัวที่น้อย (SMALL DISPLACEMENT) โดยที่วัสดุที่ใช้ในการก่อสร้างโครงสร้างคานนั้นเป็นวัสดุที่เป็นไปตามกฎของฮุค (HOOK’S LAW) และ เป็นการพิจารณาสภาวะของโครงสร้างอยู่ในช่วงที่เป็นเชิงเส้น (LINEAR ELASTIC) นะครับ โดยเรามาเริ่มต้นดูกันที่ BENDING CURVATURE กันก่อนเลยนะครับ
เนื่องจากการโก่งตัวที่เกิดขึ้นในคาน และ เนื่องจากการโก่งตัวมีค่าน้อย เราจะสามารถพิจารณาให้สามเหลี่ยม bcd และ oba นั้นเป็นสามเหลี่ยมที่มีขนาดเล็กๆ เราจะสามารถคำนวณหาค่าความเครียด (STRAIN) ได้จากความสัมพันธ์ของสามเหลี่ยมคล้ายนะครับ และ สุดท้ายค่า STRAIN จะสามารถคำนวณออกมาได้เท่ากับ
ε = cd / ab = Y / p [1]
จากกฎของฮุคเราทราบดีว่าค่า
ε = σ / E [2]
เราจะนำ [2] แทนลงใน [1] จะได้ว่า
Y / p = σ / E
σ = Y E / p [3]
และ
p = Y E / σ [4]
เราจะเห็นได้ว่าจาก [3] ค่า σ นั้นจะเป็นค่าที่เป็นสัดส่วนต่อค่าความลึกของหน้าตัด (Y) จากแกน N.A. นั้นเองนะครับ จากนั้นเรามาลองพิจารณาพื้นที่เล็กๆ ในรูปก่อนนะครับ โดยที่ dF จะเป็นส่วนองค์ประกอบ FORCE เล็กๆ ในหน้าตัดคานของเรานะครับ
dF = σ dA [5]
เราจะทำการแทน [3] ลงใน [5] นะครับ
dF = (Y E / p) dA [6]
ค่าโมเมนต์ดัดที่กระทำรอบ N.A. จะสามารถหาได้จาก
M = ∫ Y dF [7]
เราจะทำการแทน [6] ลงใน [7] นะครับ
M = ∫ Y (Y E / p) dA = (E/p) ∫ Y^(2) dA [8]
จากความสัมพันธ์ที่ว่าค่าโมดูลัสความเฉื่อย (MOMENT OF INERTIA) นั้นมีค่าเท่ากับ
I = ∫ Y^(2) dA [9]
เราจะทำการแทน [9] ลงใน [8] นะครับ
M = (E/p) I = E I / p [10]
และ
p = E I / M [11]
เราจะทำการแทน [4] ลงใน [11] นะครับ
Y E / σ = E I / M
σ = M Y / I [12]
จากนั้นจากที่เราทราบดีว่าค่า σ นั้นจะเป็นค่าที่เป็นสัดส่วนต่อค่าความลึกของหน้าตัด ![]() (Y) จากแกน N.A. ดังนั้นค่า σ max ก็จะมีค่าเท่ากับ
(Y) จากแกน N.A. ดังนั้นค่า σ max ก็จะมีค่าเท่ากับ
σ max = M C / I [13]
เราจะทำการแทน [10] ลงใน [13] นะครับ
σ max = (E I / p) C / I
σ max = E C / p [14]
ดังนั้นค่า CURVATURE ของคานจะมีค่าเท่ากับ
k = 1 / p [15]
สุดท้ายเราสามาถจะทำการแทน [15] ลงใน [14] นะครับ
σ max = E C k [16]
จาก [16] เราจะเห็นได้ว่า หากเราทราบว่าคานของเรานั้นมีค่า p เท่ากับเท่าใด เราก็สามารถที่จะหาค่า σ และ σ max ได้เช่นเดียวกันนะครับ
ในวันพรุ่งนี้ผมจะขออนุญาตมาทำการยก ตย ให้แก่เพื่อนๆ ได้ทราบกันถึงวิธีในการคำนวณหาค่า p นี้ในการแทนค่าหาค่า σ และ σ max ในโครงสร้างคานรับแรงดัดกันบ้างนะครับ เพื่อนๆ ท่านใดสนใจก็สามารถติดตามกันได้นะครับ
วันนี้ผมจะขออนุญาตมาตอบคำถามให้แก่รุ่นพี่วิศวกรที่ผมเคารพรักท่านหนึ่งที่ท่านได้กรุณาสอบถามผมมาเกี่ยวกับเรื่อง
หวังว่าความรู้เล็กๆ น้อยๆ ที่ผมได้นำมาฝากแก่เพื่อนๆ ทุกๆ ท่านในวันนี้จะมีประโยชน์ต่อทุกๆ ท่านไม่มากก็น้อย และ จนกว่าจะพบกันใหม่นะครับ
ref : https://www.facebook.com/bhumisiam/posts/1534156276630492
BSP-Bhumisiam
ผู้ผลิตรายแรก SPUN MICRO PILE
1) ได้รับมาตรฐาน มอก. มาตราฐาน397-2524 เสาเข็ม Spun Micro Pile
2) ผู้ผลิต Spun Micro Pile ที่ได้รับ Endorsed Brand รับรองคุณภาพมาตราฐาน จาก SCG
3) ผู้นำระบบ Computer ที่ทันสมัยผลิต เสาเข็ม Spun Micro Pile
4) ลิขสิทธิ์เสาเข็ม Spun Micro Pile
5) เทคโนโลยีการผลิต จากประเทศเยอรมันนี
6) ผู้ผลิต Spun Micro Pile แบบ “สี่เหลี่ยม”
7) การผลิตคอนกรีตและส่วนผสม ใช้ Program SCG-CPAC
เสาเข็ม สปันไมโครไพล์ ช่วยแก้ปัญหาได้เพราะ
1) สามารถทำงานในที่แคบได้
2) ไม่ก่อให้เกิดมลภาวะทางเสียง
3) หน้างานสะอาด ไม่มีดินโคลน
4) สามารถรับน้ำหนักได้ 20-40 ตัน/ต้น
5) สามารถตอกชิดกำแพง ไม่ก่อให้โครงสร้างเดิมเสียหาย
สนใจติดต่อสินค้า เสาเข็ม ไมโครไพล์ (Micropile)
สปันไมโครไพล์ (Spun MicroPile) มาตรฐาน มอก.
ติดต่อ สายด่วน โทร :
081-634-6586
082-790-1447
082-790-1448
082-790-1449